Find the short side of a triangle given a hypotenuse of 10 units Find the hypotenuse given a long side of 6 units Triangles are classified as "special right triangles" They are special because of special relationships among the triangle legs that allow one to easily arrive at the length of the sides with exact answers instead of decimal approximations when using trigFind the remaining sides of a 30°–60°90° triangle if 39 The shortest side is 1 40 "The shortest side is 3 41 The longest side is 8 42 The longest side is 5 43 The longest side is 44 'The longest side is 24 45 The medium side is 3V3 46 "The medium side is 2V3 47 The medium side is 6 48 The medium side is 4How To Find Sides Of A 30 60 90 Triangle 30 60 90 Triangle Therom Slidedocnow 30 60 90 Triangle Theorem Ratio And Formula Video Triangles On Sat Math Geometry Strategies And Practice How To Find The Sides Of A 30 60 90 Right Triangle Math Understanding 30 60 90 Triangles High School Math 30 60 90 Triangles Kates Math Lessons An Appearance Of A 30

The 30 60 90 Triangle Topics In Trigonometry
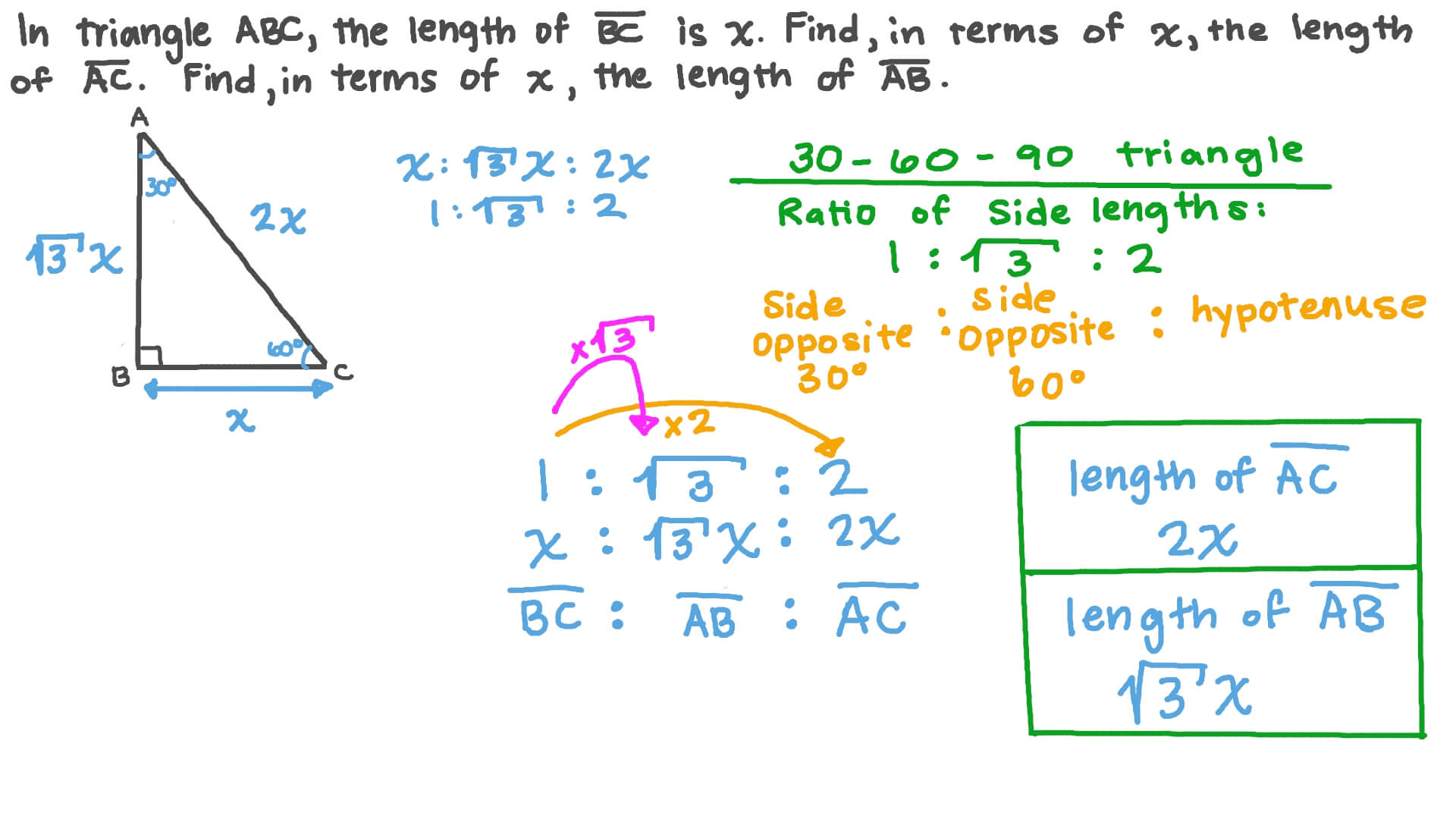
Find the sides of a 30 60 90 triangle
Find the sides of a 30 60 90 triangle-Find the remaining sides of a 30° – 60° – 90° triangle if the longest side is 9 The side opposite 60° is and the shortest side is ;Special Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangle



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures
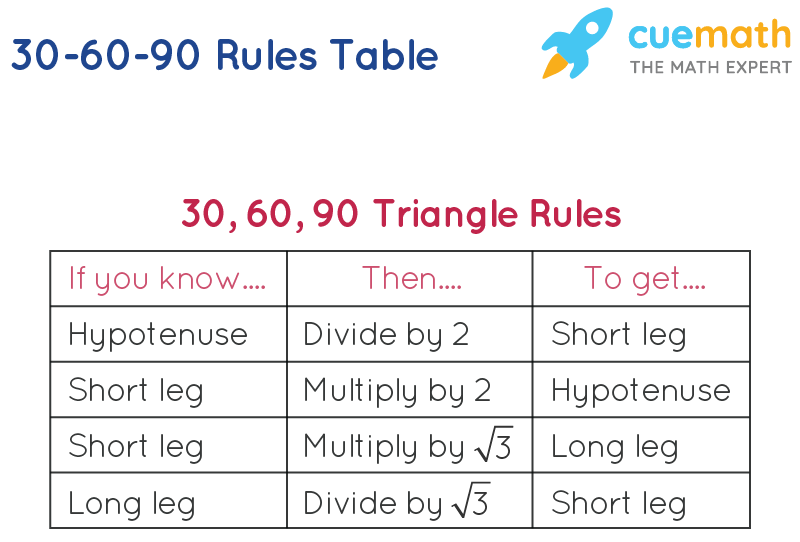
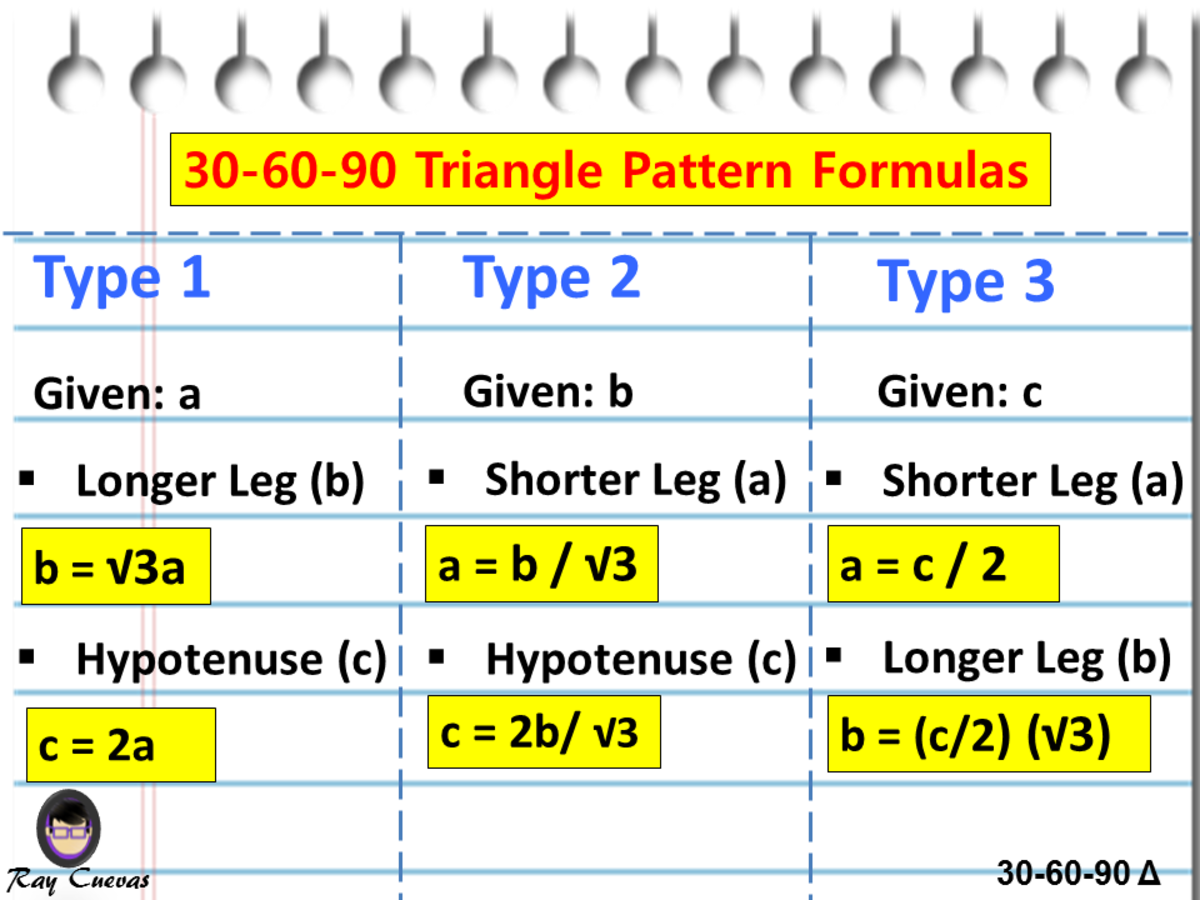
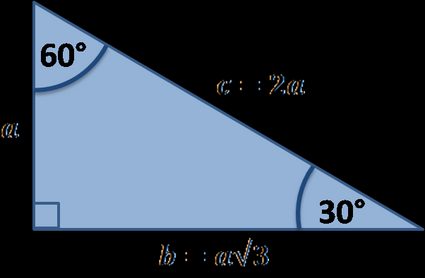
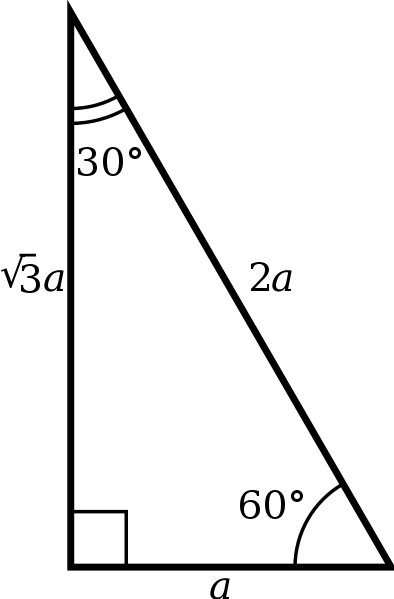
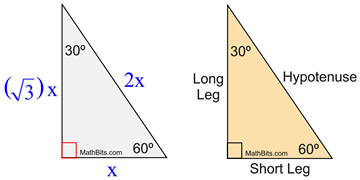
30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 All degree triangles have sides with the same basic ratio Two of the most common right triangles are and degree triangles If you look at the 30–60–90degree triangle in radians, it translates to the following In any triangle, you see the following The shortest leg is across from the 30degree angle The three sides are 4, 4sqrt(3), and 8 The ratio of the sides in a triangle is xxsqrt(3)2x That means if the side opposite 30^circ is x, then the side opposite 60^circ is xsqrt(3) and the side opposite 90^circ is 2x Since the longest side is the hypotenuse, which is opposite 90^circ, we know that 2x = 8\rightarrow x = 4
Question Find the remaining sides of a 30° – 60° – 90° triangle if the longest side is 9 The side opposite 60° is and the shortest side isIt doesn't matter which30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2a Worksheet 45 ¡45 ¡90 triangleand30 ¡60 ¡90 triangle 1For the 45 ¡45 ¡90 triangle, (the isosceles right triangle), there are two legs of length a and the
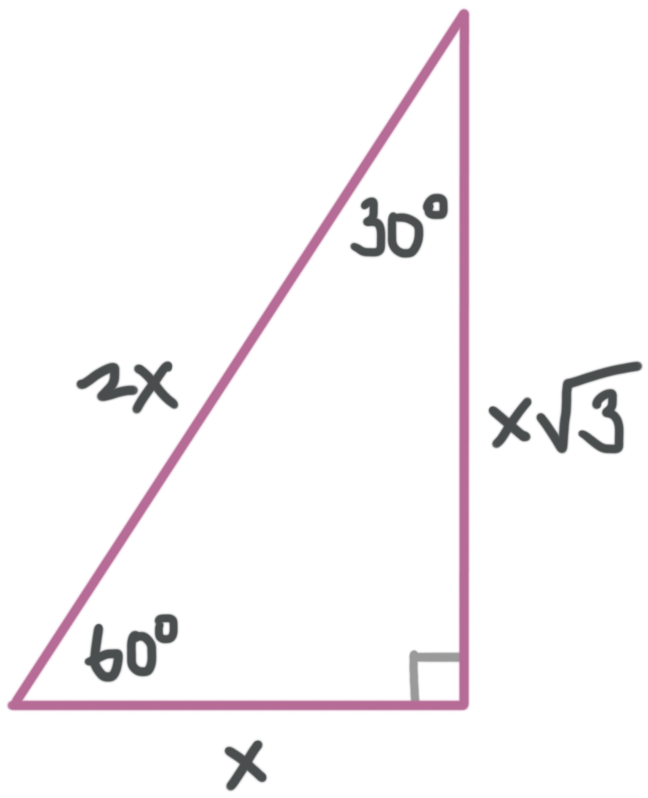
The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a 2 b 2 = c 2 a 2 (a√3) 2 = (2a) 2 a 2 3a 2 = 4a 2 ADVERTISEMENT 4a 2 = 4a 2 Notice that these ratios30°60°90° triangle The 30°60°90° refers to the angle measurements in degrees of this type of special right triangle In this type of right triangle, the sides corresponding to the angles 30°60°90° follow a ratio of 1√ 32 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be determinedIn a triangle, the ratio of the sides is always in the ratio of 1√3 2 This is also known as the triangle formula for sides yy√32y Let us learn the derivation of this ratio in the triangle proof section Consider some of the examples of a degree triangle with these side lengths Here, in the triangle DEF ∠ F = 30°, ∠ D = 60°, and




30 60 90 Triangle Theorem Ratio Formula Video



How To Solve 30 60 90 Triangles Krista King Math Online Math Tutor
–find the distance in a 30, 60, 90 triangle 1 answer below » a symmetrical canyon is 4850 feet deep a river runs through the canyon at its deepest point the angle of depression from each side of the canyon to the river is 60o round to theExample of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units inOther interesting properties of triangles are All triangles are similar;




A Triangle With Angle Measures 30 60 90 Has A Perimeter Of 18 6 3 Pwn Test Prep



Pythagorean Triples
Two triangles sharing a long leg form an equilateral triangle;Given the triangle below, find the lengths of the missing sides Since this is a right triangle, we know that the sides exist in the proportion 1\(\sqrt{3}\)2 The shortest side, 1, is opposite the 30 degree angle Since side X is opposite the 60 degree angle, we know that it is equal to \(1*\sqrt{3}\), or about 173Click here👆to get an answer to your question ️ In a 30 60 90 triangle, the length of the hypotenuse is 6 What is the length of the shortest side?




30 60 90 Triangle Explanation Examples
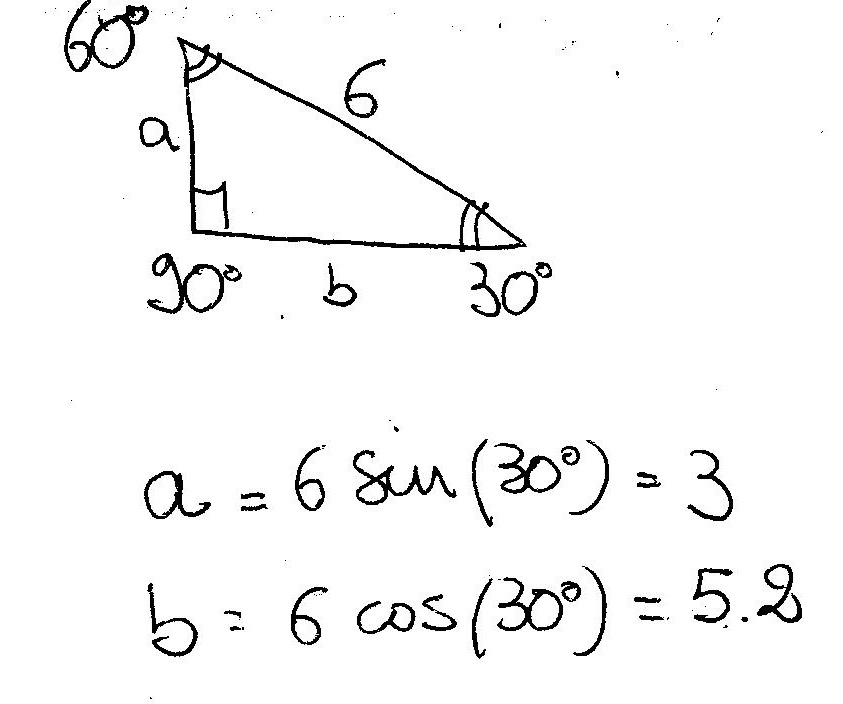



How Do You Find The Remaining Sides Of 30 Circ 60 Circ 90 Circ Triangle If The Longest Side Is 6 Socratic
The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion ofAnswer (1 of 3) This question definitely needs to be edited first I guess the question is Q What is the formula to find the hypotenuse in a 30 60 90 triangle If the question is as above FORMULA HYPOTENUSE = √{ s² (√3 s)²}, where s is a side length of the right triangle And obviouAnswer (1 of 3) How do I find the missing sides in special right triangles using the 30–60–90 rule?




30 60 90 Right Triangles Ck 12 Foundation




Relationships Of Sides In 30 60 90 Right Triangles Read Geometry Ck 12 Foundation
How to Solve a Triangle Education is knowing that triangles have three properties laidPractice Using the Triangle to Find Side Lengths with practice problems and explanations Get instant feedback, extra help and stepbyIt turns out that in a triangle, you can find the measure of any of the three sides, simply by knowing the measure of at least one side in the triangle The hypotenuse is equal to twice the length of the shorter leg, which is the side across from the 30 degree angle



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures
Check out this tutorial to learn about triangles! A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherFind the area of a triangle whose sides are 26 cm, 28 cm and 30 cm If two acute angles of a right triangle are equal,then each acute is equal to 30^(0) (b) 45^(@) (c) In a rightangled triangle ABC, angleB=90^(@), angleA=30^(@) and AC = cm Determine the lengths o



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa




30 60 90 Triangle Calculator Formula Rules
Find the missing side lengths And Triangle Worksheet Special right triangles 45 45 90 worksheet answers, ALQURUMRESORTCOM Explains a simple pictorial way to remember basic reference angle values Most trig questions you've done up till now Leave your answers as radicals in simplest form G o xm6awdyea awsiutwh7 eidnrf8i7nvi8t6eg30 60 90 Triangle "Short Side", "Medium Side" or "Hypotenuse" 45 45 90 Triangle "Side" or "Hypotenuse" As soon as you click that box, the output boxes will automatically get filled in by the calculator Clicking "RESET" clears all of the boxes Special Right Triangles A special right triangle is one which has sides or angles for which simple formulas exist making calculations easy Of allThis rule only works for right triangles whose other internal angles are 30° and 60° respectively Further, for the rule to work, you need to know the length of one side;



A 30 60 90 Triangle



5 5 Special Triangles
Triangle in trigonometry In the study of trigonometry, the triangle is considered a special triangleKnowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angles 30° and 60° For example, sin(30°), read as the sine of 30 degrees, is the ratio of the sideAnswer to Find the remaining sides of a 30, 60, 90 triangle if the opposite side of 60 degrees is 6 By signing up, you'll get thousands ofFind the sides on this triangle 50 points in it for you plus a thanks, 5 star and brainliest (suggested to have a fast answer) Answers 3 Get Other questions on the subject Mathematics Mathematics, 1430, kana13 Geometry determine whether segment mn is parallel to segment kl justify your answer jm 6 mk 3 jn 8 nl 4




Math Journals Triangle Trigonometry



30 60 90 Triangle Rules
If you know the length of any one side of a triangle, you can find the missing side lengths; Properties of and triangles An equilateral triangle is one in which all three sides have equal lengths (a) Prove that a Euclidean triangle is equilateral if and only if each of its angles measures 60A triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!



1



1
THE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that below Find out what are the sides, hypotenuse, area and perimeter of your shape and learn about 45 45 90 triangle formula, ratio and rules If you want to know more about another popular right triangles, check out this 30 60 90 triangle tool and the calculator for special right triangles



Long Leg Of Right Triangle




The Complete Guide To The 30 60 90 Triangle



30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Example Problem Video Khan Academy




Instructions Use The Ratio Of A 30 60 90 Triangle To Solve For The Variables Leave Your Answers As Brainly Com




30 60 90 Right Triangles Solutions Examples Videos




How To Use The Special Right Triangle 30 60 90 Studypug



The Easy Guide To The 30 60 90 Triangle




Special Right Triangles Part 3 30 60 90 Youtube




A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangles Spock S Guide To Math 4



30 60 90 Triangle Formulas Rules And Sides Science Trends



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




How How Do I Find The Measure Of The Sides Of An Equilateral Triangle Inscribed In A 30 60 90 Triangle Mathematics Stack Exchange



How To Find The Legs Of A 30 60 90 Triangle Quora
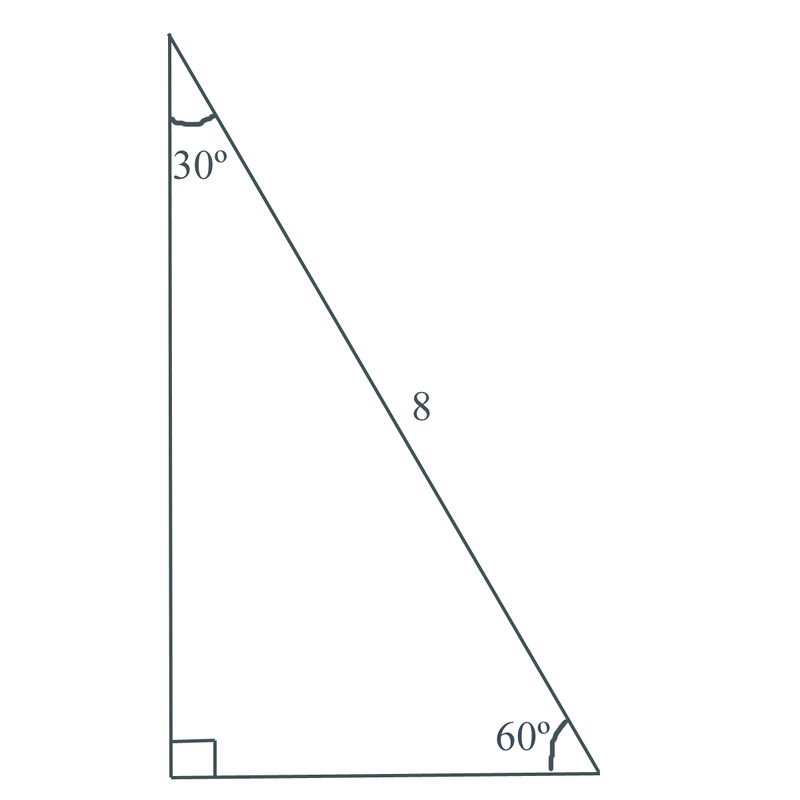



Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Right Triangles Free Math Help
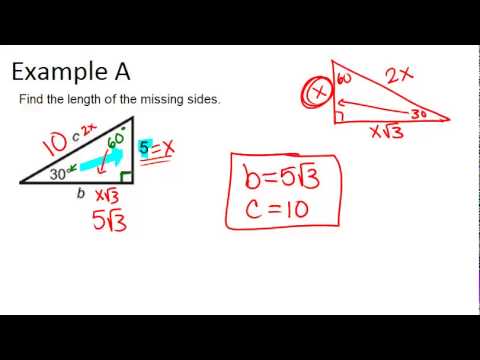



30 60 90 Right Triangles Examples Geometry Concepts Youtube
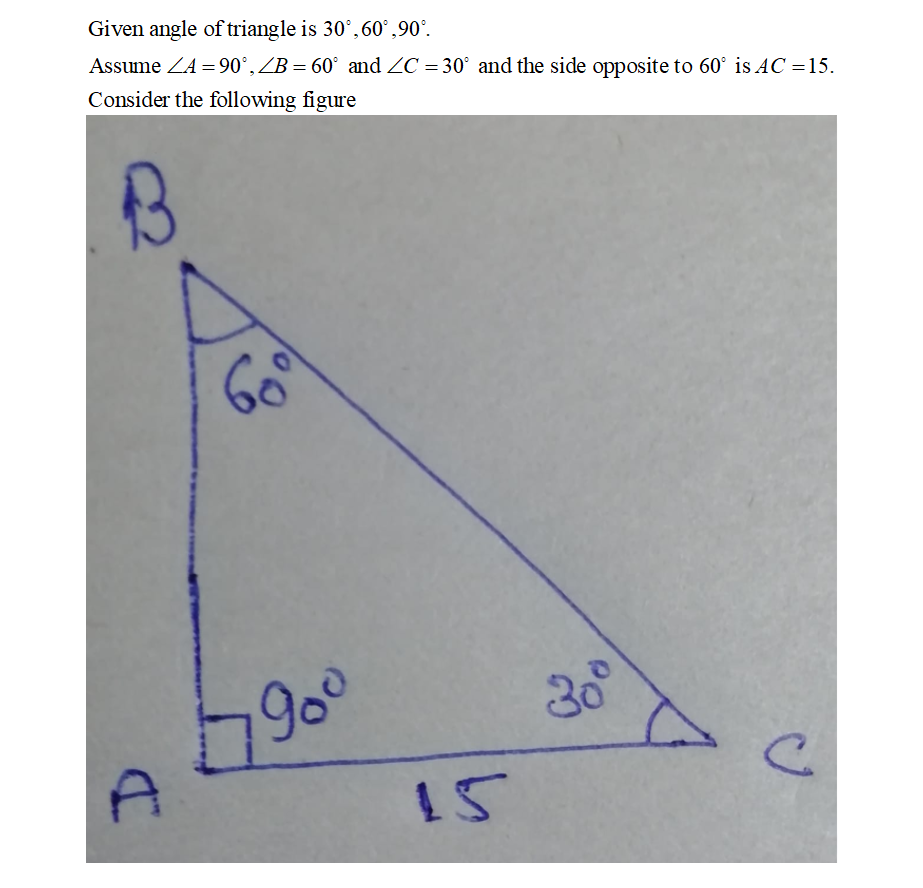



Answered Find The Remaining Sides Of A Bartleby



Solution In A Triangle Abc Angle A 30 Angle B 90 And Ab Is 12 Cm Find The Length Of
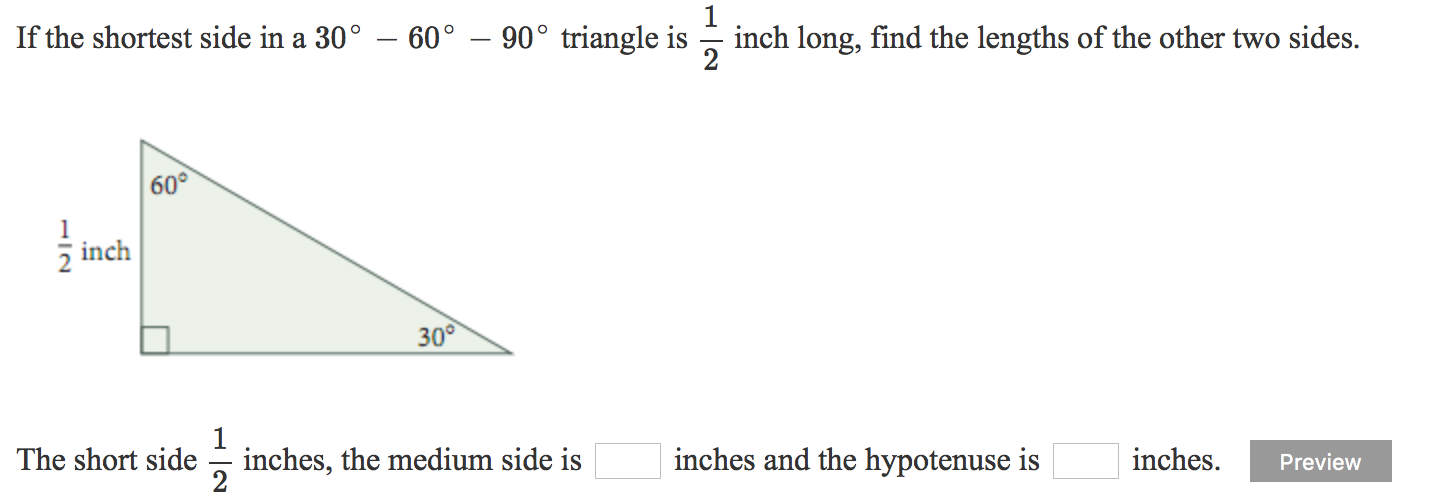



Solved If The Shortest Side In A 30 60 90 Triangle Is Z Chegg Com




The 30 60 90 Triangle Topics In Trigonometry




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




A Quick Guide To The 30 60 90 Degree Triangle Dummies




He Length Of The Hypotenuse Of A 30 60 90 Triangle Is 13 Meters Find The Length Of The Side Brainly Com




Solved 1 For A 30 60 90 Triangle It Is Known That The Chegg Com
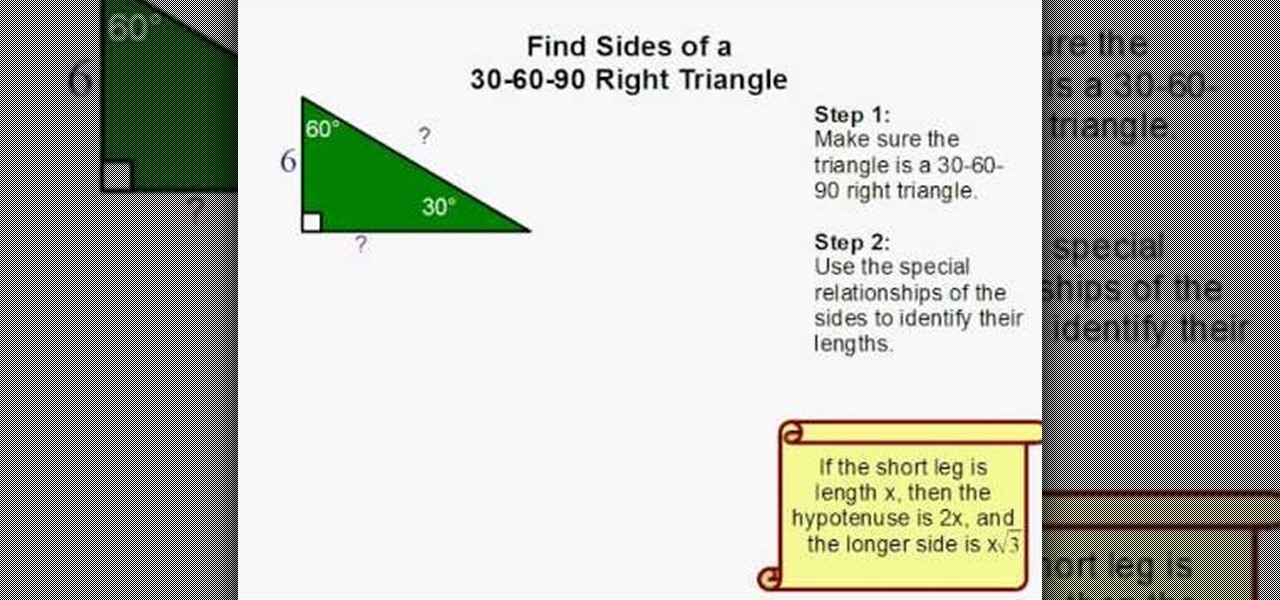



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto




5 30 60 90 Triangles Geometry15a




Lesson 6 3 6 4 Objective To Find The Two Missing Lengths Of A 30 60 90 Triangle To Classify Four Sided Polygons In A 30 60 90 Triangle The Hypotenuse Ppt Download
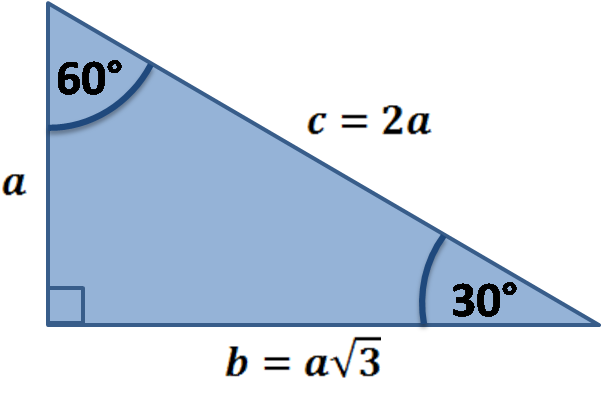



30 60 90 Triangle Calculator Online Discount Shop For Electronics Apparel Toys Books Games Computers Shoes Jewelry Watches Baby Products Sports Outdoors Office Products Bed Bath Furniture Tools Hardware




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



1




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Calculator Formula Rules
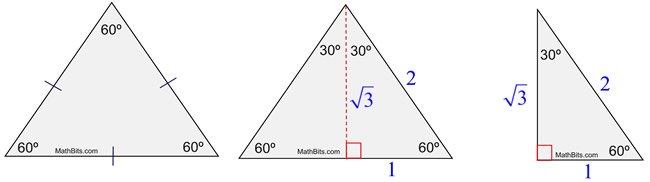



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




How To Work With 30 60 90 Degree Triangles Education Is Around
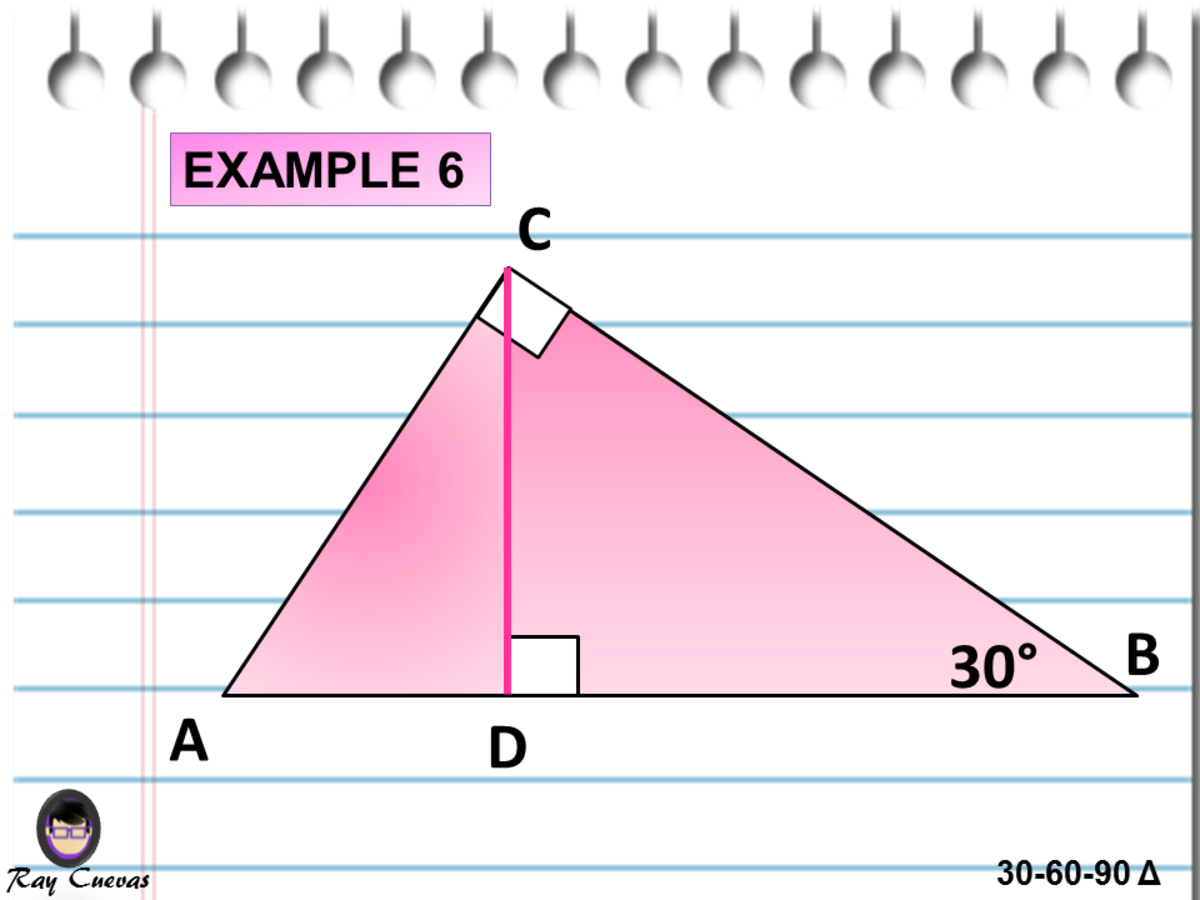



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
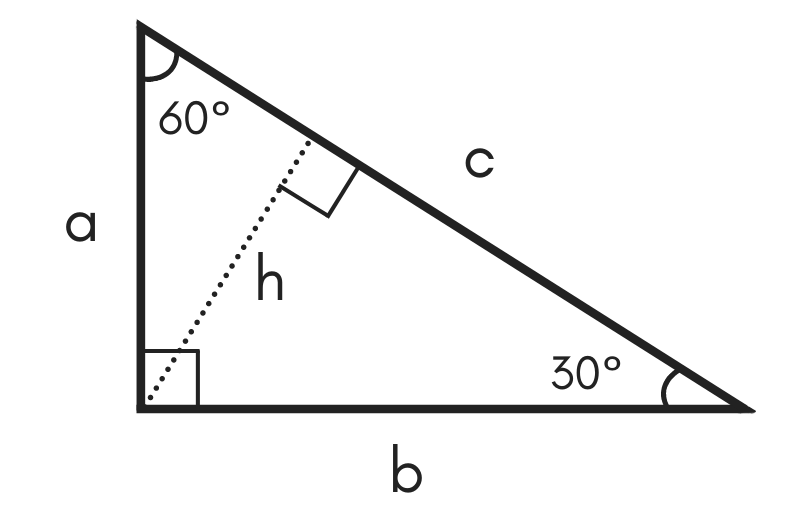



30 60 90 Special Right Triangle Calculator Inch Calculator




Finding The Missing Side Of 30 60 90 Triangle Youtube
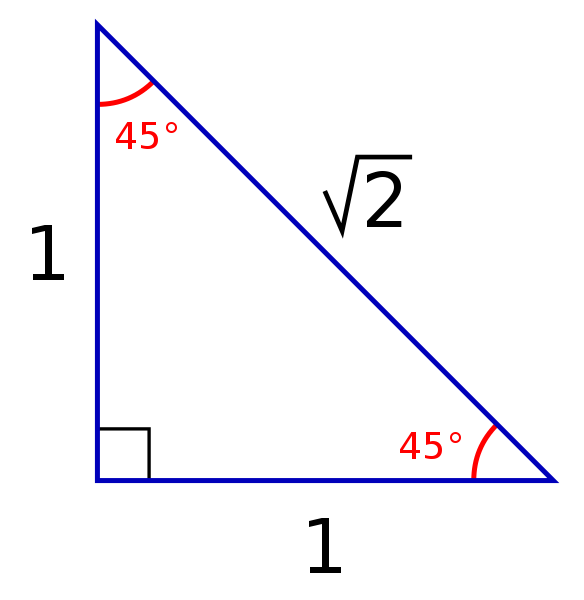



30 60 90 Triangle Formulas Rules And Sides Science Trends
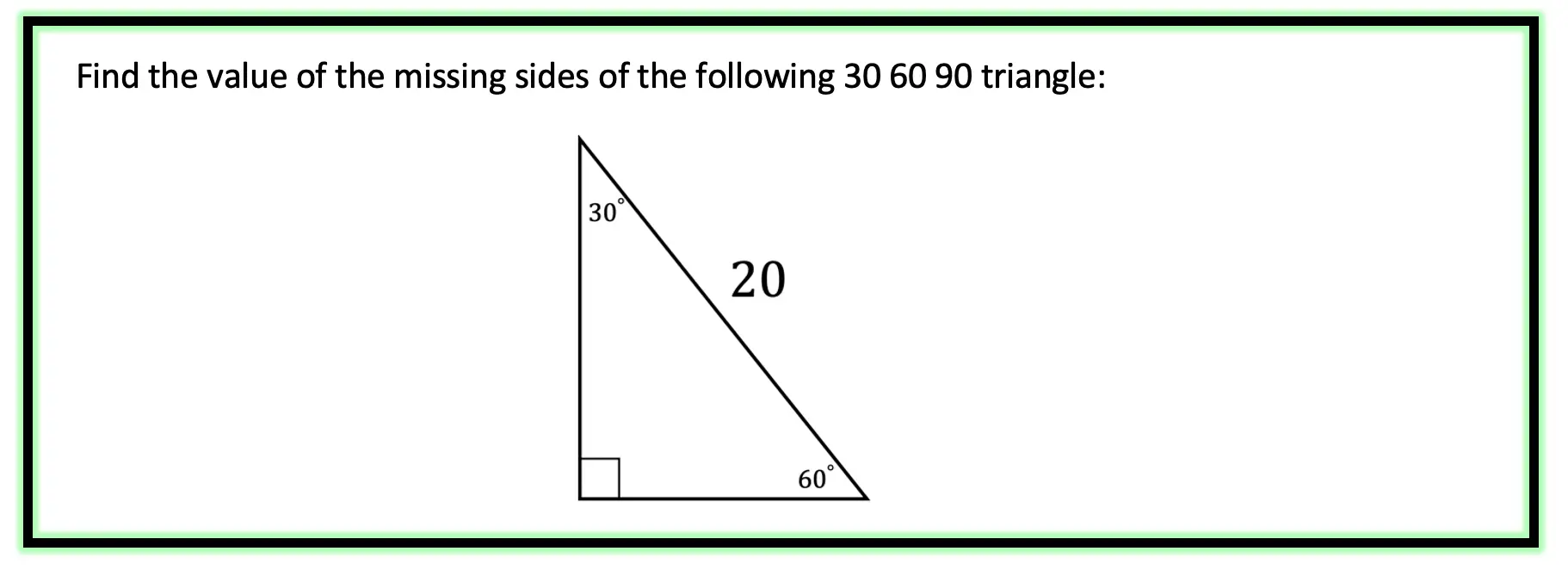



30 60 90 Special Triangles Geometry Mathsux 2



Solve A 30 60 90 Triangle With Gradea




30 60 90 Triangle Theorem Ratio Formula Video
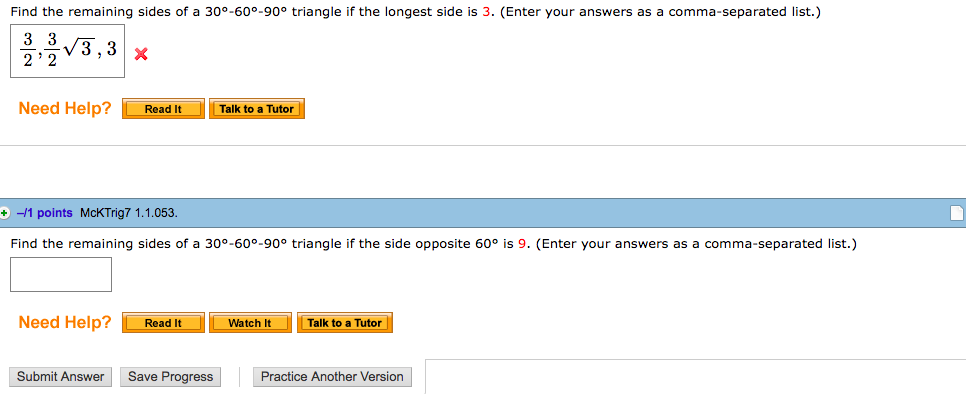



Solved Find The Remaining Sides Of A 30 60 90 Triangle If Chegg Com
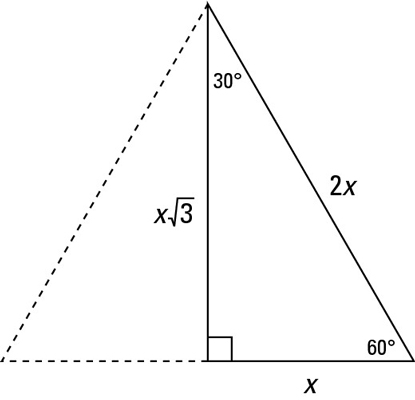



Identifying The 30 60 90 Degree Triangle Dummies
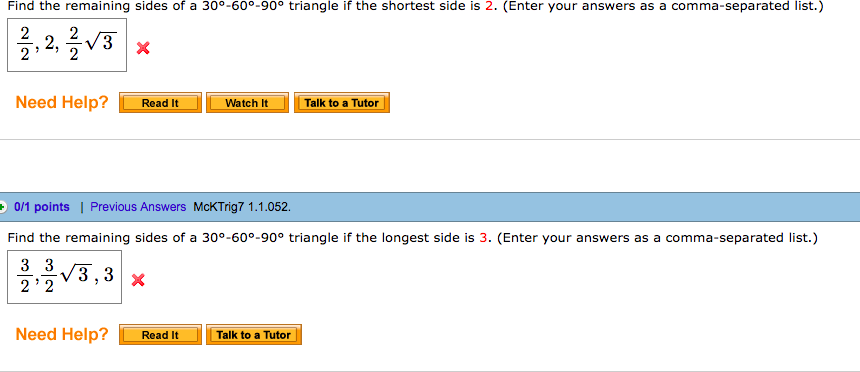



Solved Find The Remaining Sides Of A 30 60 90 Triangle If Chegg Com




30 60 90 Right Triangle Side Ratios Expii




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 And 45 45 90 Triangles Youtube



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Explanation Examples
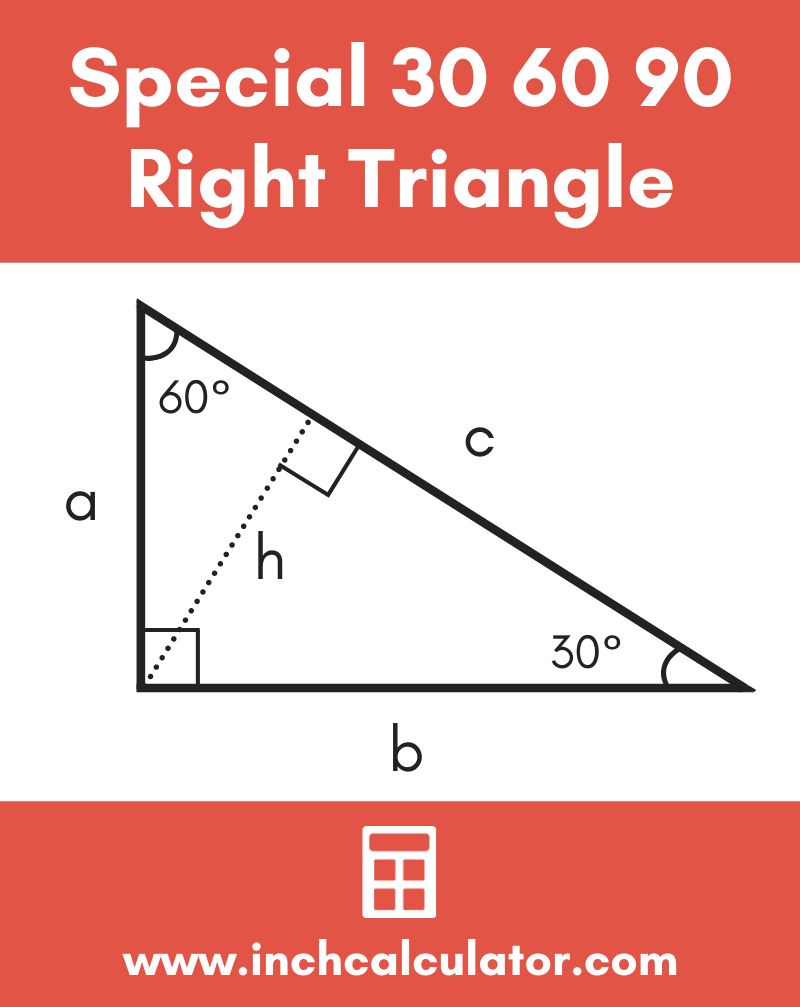



30 60 90 Special Right Triangle Calculator Inch Calculator




Special Right Triangles Video Lessons Examples And Solutions




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
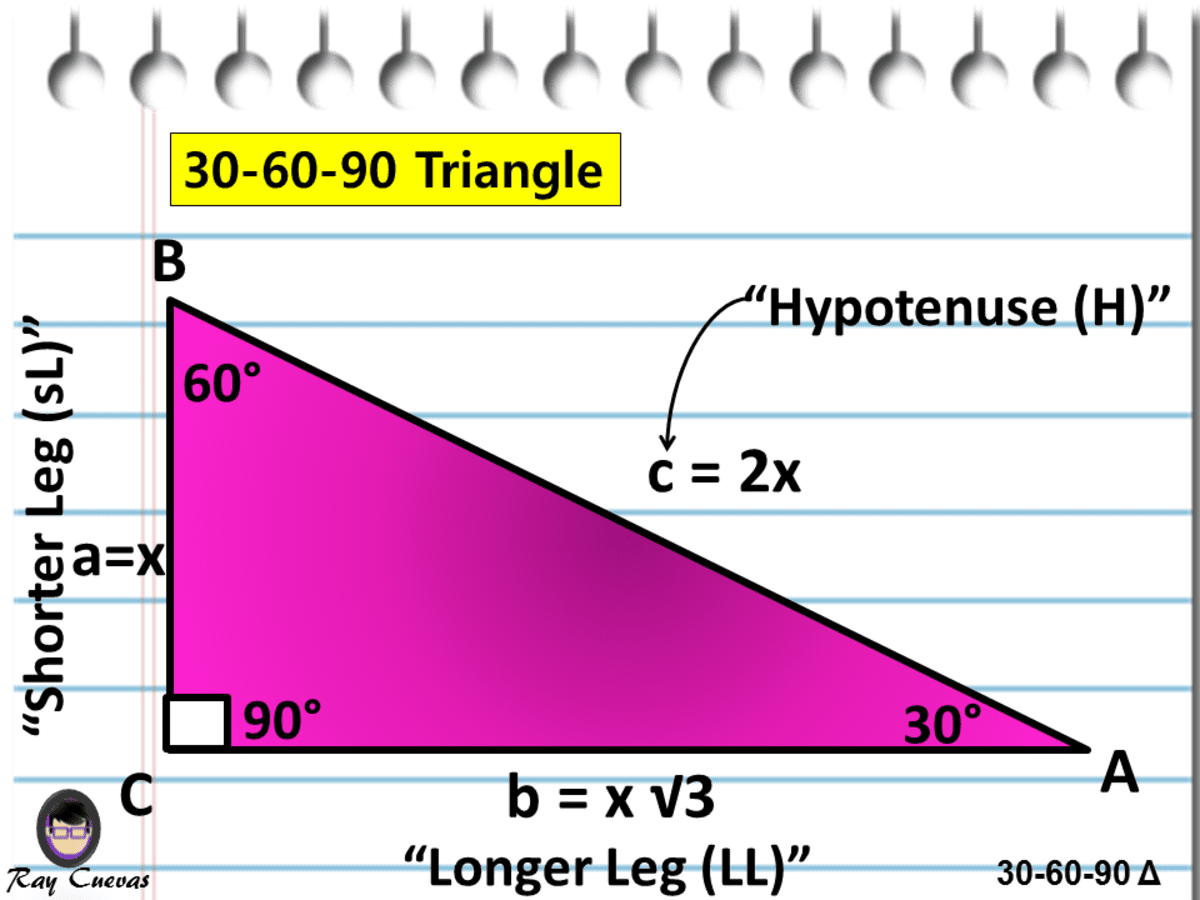



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
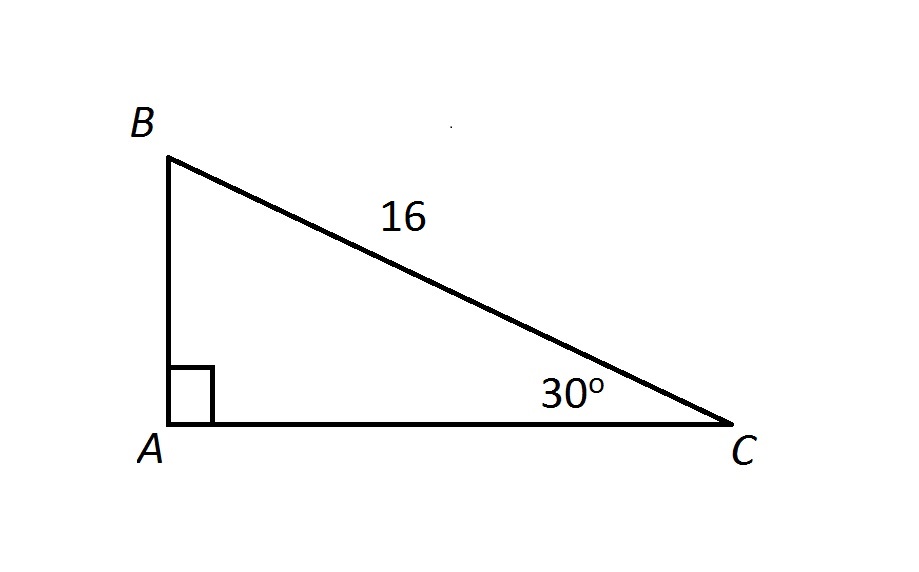



Special Triangles Hiset Math




30 60 90 Triangle Explanation Examples
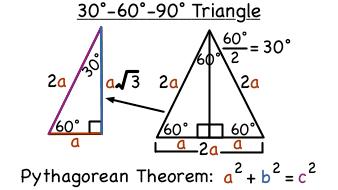



What Is A 30 60 90 Degree Triangle Virtual Nerd
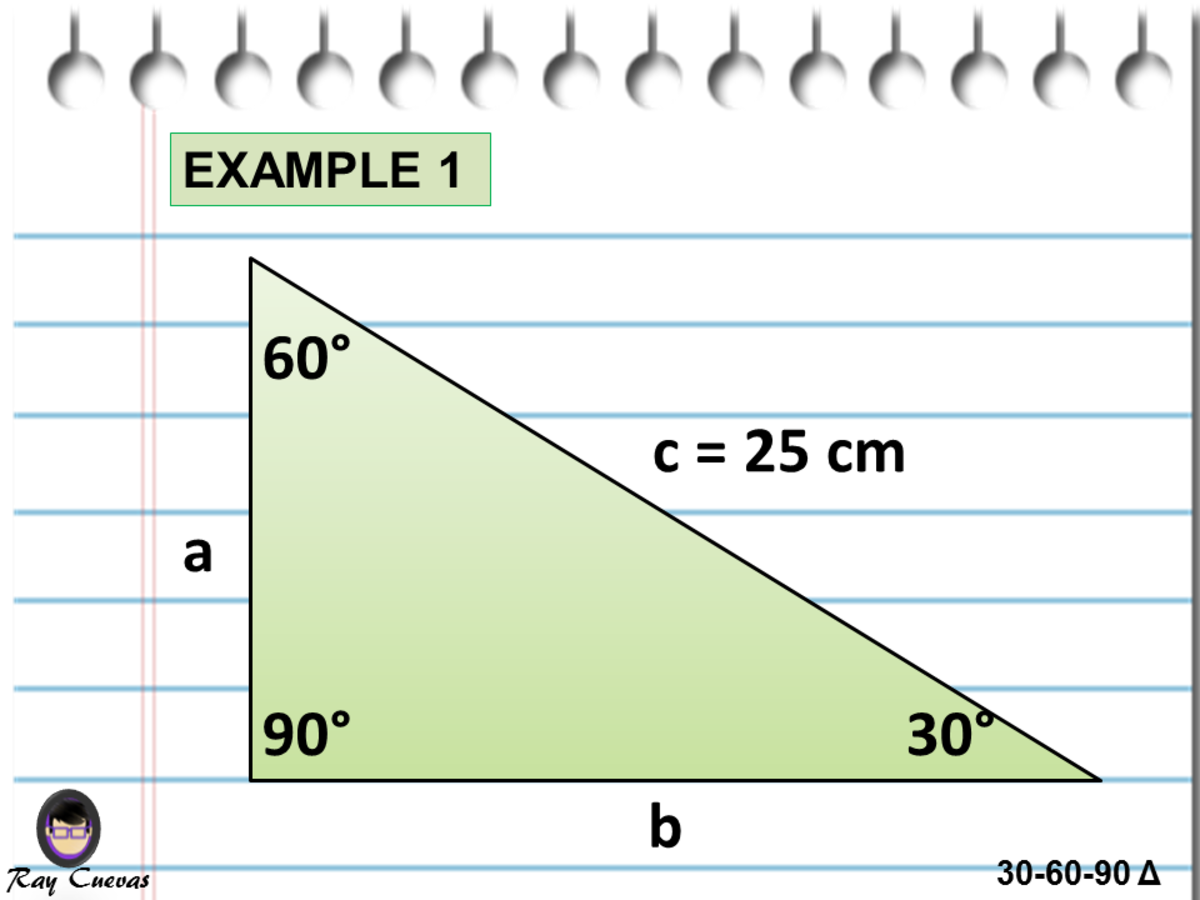



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video
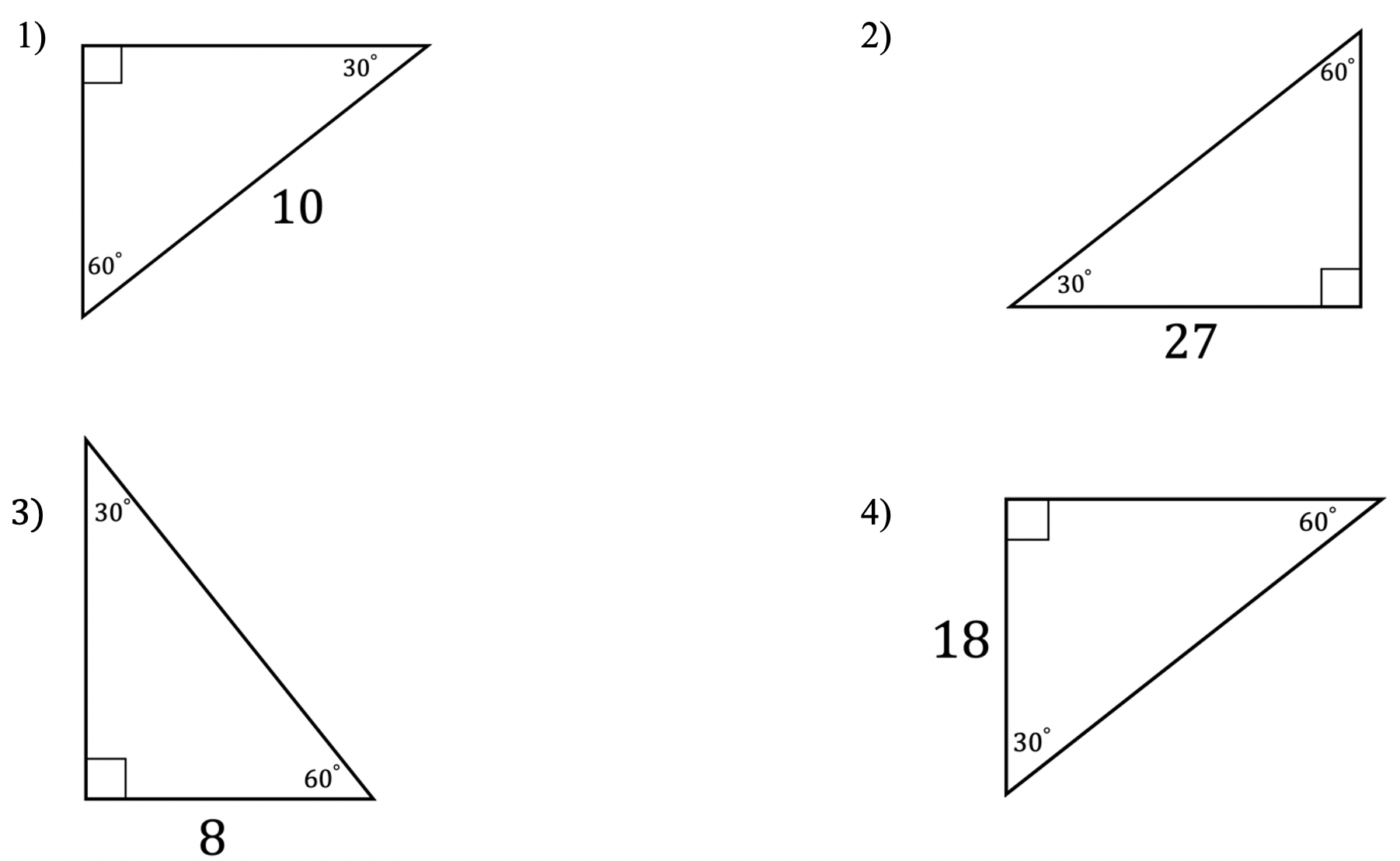



30 60 90 Special Triangles Geometry Mathsux 2



30 60 90 Triangle Formulas Rules And Sides Science Trends
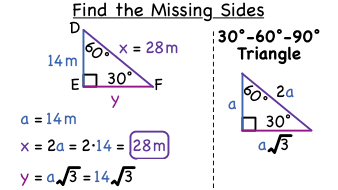



How Do You Find Missing Sides In A 30a 60a 90a Triangle Virtual Nerd




The 30 60 90 Triangle Topics In Trigonometry
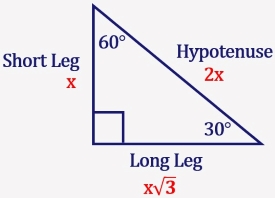



Find The Side Lengths Of A Special Right Triangle 30 60 90 Mathondemand Com




30 60 90 Triangle Theorem Ratio Formula Video




A 30 60 90 Triangle Is Shown Below Find The Length Of The Side Labeled Y Brainly Com




View Question Practice Problems 1 In A 30 60 90 Triangle What Is The Length Of The Hypotenuse When The Shorter Leg Is 8m
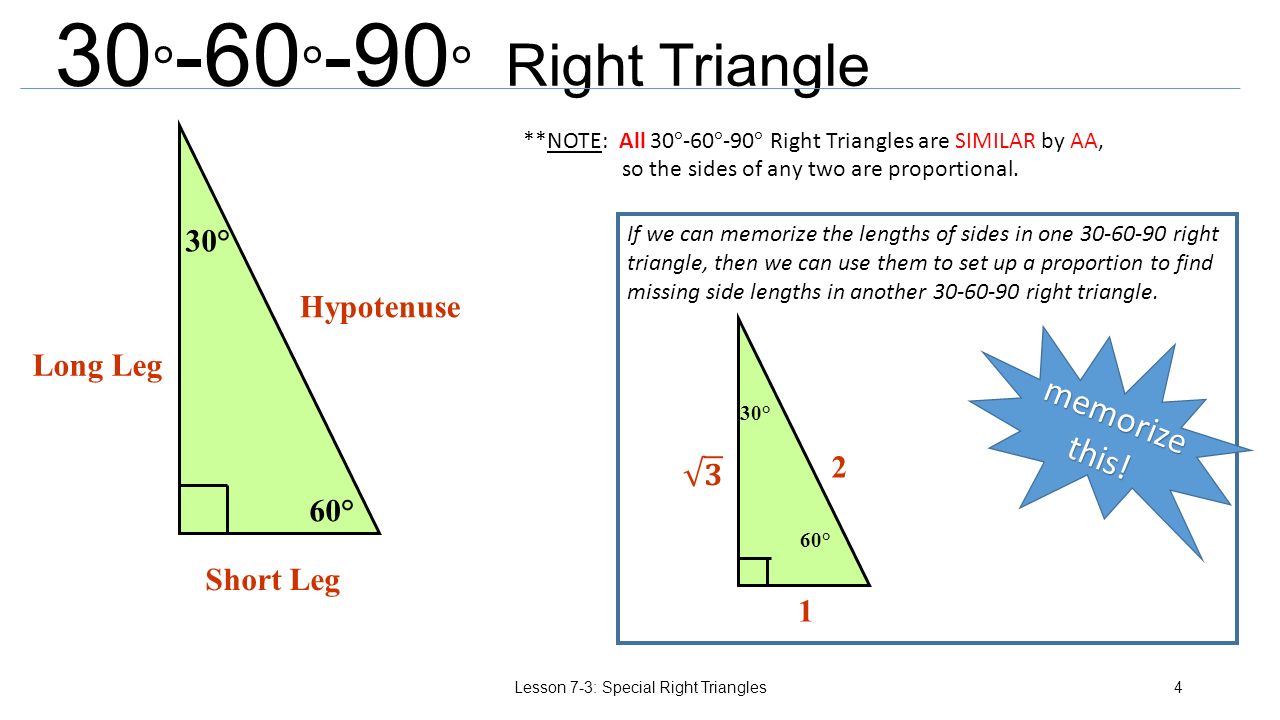



Special Right Triangles Lesson 7 3 Special Right Triangles1 Ppt Download



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangles Free Math Lessons Geometry Lessons Printable Study Guides




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Theorem Ratio Formula Video




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



5 5 Special Triangles




Special Right Triangles Ppt Video Online Download




How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto



How To Solve A 30 60 And 90 Triangle Quora
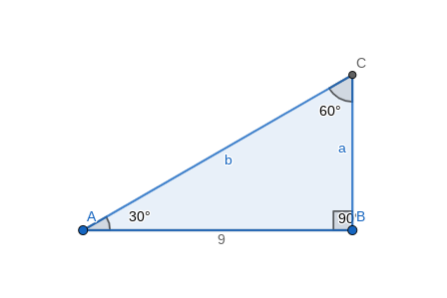



Activity 22 Construct A 30 60 90 Triangle Geogebra




30 60 90 Triangle Theorem Ratio Formula Video
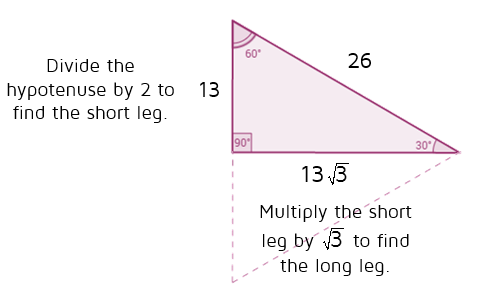



30 60 90 Triangles P4 Kate S Math Lessons
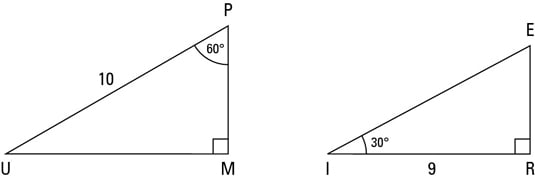



Identifying The 30 60 90 Degree Triangle Dummies




5 8b 30 60 90 Special Right Triangles Youtube
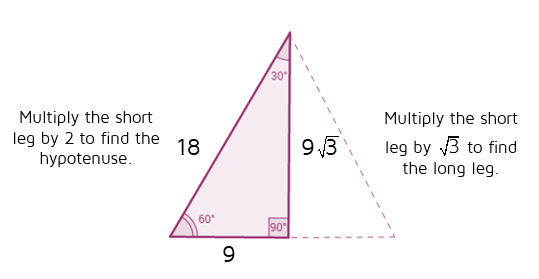



30 60 90 Triangles P4 Kate S Math Lessons


